如果沒有error correction會發生甚麼事?

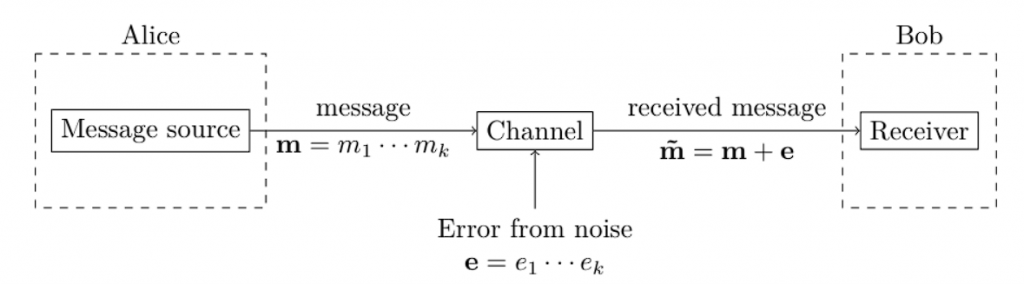
Alice想要傳輸一個長度𝑘的訊息𝐦，這是一個位元序列。當她發送它時，它會被噪音扭曲𝐞，因此Bob收到的是 = 𝐦 + 𝐞

一般來說 𝐞 可以是任何位元串，但讓我們為我們在現實世界中遇到的傳輸雜訊類型定義一個簡單而現實的模型。我們假設如果我們發送一點 𝑚𝑖 通過通道，有機率 𝑝 該位元將被翻轉，並且有機率 1 − 𝑝 它沒有翻轉。如果我們透過通道發送多個位，則每個位元都會以機率獨立翻轉 𝑝。這意味著

重複檢測和糾正

重複檢測和糾正錯誤的過程如下，將Alice發送的訊息加長，例如:Alice 原先想傳輸1給Bob，但怕傳輸中間有機會被翻轉狀態，因此Alice把訊息加長，變成111，因此往後Alice發送的訊息n，會是3倍的原先訊息。
我們給這樣的傳輸訊息定義了一個表示法如下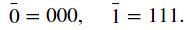

因此會等於111000111000

假設經過有噪音的通訊傳輸，Bob收到101100111000，Bob可以透過每三個位元一個區塊的方式，將101推斷為，以此類推
因此他可以正確地將訊息解碼為

程式示範

重複編碼

以下是重複編碼的過程

def repetition_encode(data_stream):
    streng=""
    for i in (data_stream):
        streng+=i*3
    return streng
# check your solution
k = 3
for i in range(2**k):
    message = bin(i)[2:].zfill(k)
    codeword = repetition_encode(message)
    print(message, codeword)    

000 000000000
001 000000111
010 000111000
011 000111111
100 111000000
101 111000111
110 111111000
111 111111111

重複解碼

以下是模擬通過有噪音的通訊並重複解碼

def repetition_decode(codeword):
    n = 3
    strength=""
    chunks = [codeword[i:i+n] for i in range(0, len(codeword), n)]
    lens=int(len(codeword)/3)
    for i in range(lens):
        if chunks[i]=="111"or chunks[i]=="110"or chunks[i]=="101"or chunks[i]=="011":
            strength+='1'
        else:
            strength+='0'
    return strength

from random import randint
import random
# these are the two parameters we need to set
message_length = 5
p = 0.1

# create a random message
message = ''.join([str(randint(0,1)) for i in range(message_length)])
print('message = ', message)

# encode the message
codeword = repetition_encode(message)
print('codeword = ', codeword)

# send it through the noisy channel
corrupted_codeword = ''
for c in codeword:
    if random.random() < p:
        if c == '0':
            corrupted_codeword += '1'
        else:
            corrupted_codeword += '0'
    else:
        corrupted_codeword += c
print('corrupted_codeword = ', corrupted_codeword)
        
# decode it
estimated_message = repetition_decode(corrupted_codeword)
print('estimated_message = ', estimated_message)
print('Is message = estimated_message?', message == estimated_message)

message = 11011
codeword = 111111000111111
corrupted_codeword = 011111000101111
estimated_message = 11011
Is message = estimated_message? True

參考資料:https://github.com/abdullahkhalids/qecft